Regression to the mean

Re­gres­sion to the mean (RTM) is the sta­tis­ti­cal ten­dency for ex­treme mea­sure­ments to be fol­lowed by val­ues closer to the mean. In sim­pler terms, things tend to even out. Most of us have an in­tu­itive grasp of this con­cept, but it’s use­ful to un­der­stand it in more depth.

Why do things tend to even out? Why do mea­sure­ments tend to­wards the mean? When should we ex­pect RTM to hap­pen? Isn’t all of this too ob­vi­ous? I’ll try to an­swer these ques­tions here.

Why do mea­sure­ments tend to­wards the mean?

Let’s con­sider a se­ries of in­de­pen­dent events. For in­stance, the score of a se­quence of dart throws. Ex­tremely low and high score are un­likely due to the typ­i­cal de­sign of dart­boards. There­fore, The dis­tri­b­u­tion of dart-​throw scores will ap­prox­i­mate a nor­mal dis­tri­b­u­tion.

Now, let’s con­sider the re­la­tion­ship be­tween two con­sec­u­tive dart throws. Since they are in­de­pen­dent, we ex­pect on av­er­age 0 cor­re­la­tion be­tween their scores. There­fore, if the first throw had a high score, we couldn’t infer any­thing about the sec­ond throw. This is the most ex­treme form of RTM, since the first mea­sure­ment has no in­flu­ence over the sec­ond one.

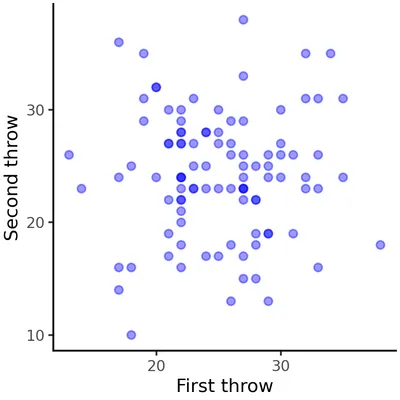
There­fore, a lucky throw doesn’t change the prob­a­bil­ity of get­ting ex­treme (high or low) scores on the next throw. The score of the sec­ond throw will be cen­tered — of course — around the mean, re­gard­less of the first score.

This ex­am­ple may seem use­less, but it lies on the heart of RTM. Val­ues tend to regress to the mean sim­ply be­cause the mean is the most likely value when the vari­able is ap­prox­i­mately nor­mally dis­trib­uted. The nor­mal­ity as­sump­tion may seem re­stric­tive, but a huge num­ber of things are some­what nor­mally dis­trib­uted. Even when the dis­tri­b­u­tion is skewed, some form of re­gres­sion still hap­pens.

Re­gres­sion be­tween cor­re­lated mea­sure­ments

Per­fectly cor­re­lated vari­ables

Con­sider you are a physi­cian tak­ing a look at pa­tient records. You no­tice that for many pa­tients there are two mea­sure­ments of their height and de­cide to plot these two val­ues to­gether. Con­sider there is no error when mea­sur­ing height. You should get some­thing like this:

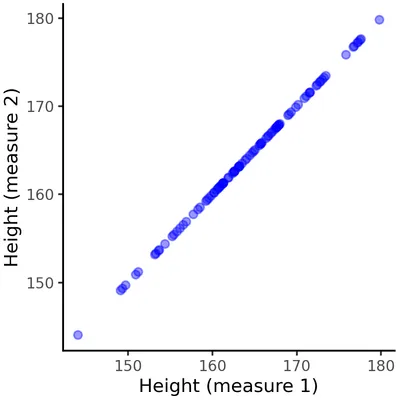
Since both mea­sure­ments cap­ture the same value (pa­tient height), they are per­fectly cor­re­lated. In this case, there is no RTM. Know­ing the value of one mea­sure­ment com­pletely de­ter­mines the value of the other, there­fore ex­treme val­ues in the first mea­sure­ment re­main ex­treme in the sec­ond one. In fact, it hardly makes sense to talk about RTM in this case, since there are no truly in­de­pen­dent val­ues be­tween which the value may regress to the mean. Still, it’s im­por­tant to un­der­stand that RTM doesn’t hap­pen in this sce­nario and why.

The ex­am­ple is very spe­cific be­cause there are al­most no (if any) two real-​world mea­sure­ments with per­fect cor­re­la­tion, ex­clud­ing those that ex­press the same un­der­ly­ing value. Thus, al­most all pairs of vari­ables or mea­sure­ments ei­ther have par­tial cor­re­la­tion or no cor­re­la­tion at all. When there is no cor­re­la­tion, we’ve seen that RTM hap­pens at its max­i­mum. When there is par­tial cor­re­la­tion, RTM hap­pens with a smaller mag­ni­tude. There­fore, if you pick two ran­dom vari­ables RTM is al­most cer­tainly at play.

Fran­cis Gal­ton and heights

Fran­cis Gal­ton first de­scribed what we now know as re­gres­sion to the mean while an­a­lyz­ing heights of par­ents and chil­dren. He no­ticed that very tall par­ents usu­ally have shorter chil­dren and vice-​versa. Even though our un­der­stand­ing of ge­net­ics was lack­ing at the time, this ob­ser­va­tion laid the foun­da­tion to the con­cept of RTM and re­gres­sion analy­sis more gen­er­ally.

There is noth­ing par­tic­u­lar about the av­er­age height that dri­ves chil­dren to­wards it. Rather, due to the com­plex na­ture of hered­ity, the cor­re­la­tion be­tween par­ents’ height and chil­dren’s height is not per­fect and so RTM hap­pens. Why? Well, start­ing with the dart throw ex­am­ple, the mean is the most likely value for a normal-​ish dis­tri­b­u­tion. Since there is a cor­re­la­tion, taller par­ents have taller kids on av­er­age. But since the cor­re­la­tion is not per­fect, there is a sig­nif­i­cant ran­dom el­e­ment, which re­sem­bles the dart throw. That is, the height of the par­ents only par­tially pre­dict the height of the chil­dren, and the ran­dom con­tri­bu­tion pulls val­ues to­wards the mean.

There are some ways to in­tu­itively grasp this con­cept. We can think that ex­treme val­ues are out­liers and, as such, are too un­likely to hap­pen mul­ti­ple times. Or we can think that the mean is a very rea­son­able most-​likely value, and we drift away from the mean given a prior ob­ser­va­tion pro­por­tion­ately to the strength of the cor­re­la­tion.

Placebo ef­fect

Even though the placebo ef­fect is widely known, it’s often mis­rep­re­sented. The placebo ef­fect is ob­served in med­i­cine and clin­i­cal tri­als when a placebo (an inert med­ical in­ter­ven­tion, e.g. sugar pills) pro­duces an ap­par­ent im­prove­ment of some symp­toms or even ob­jec­tive mea­sure­ments cor­re­lated with dis­ease sta­tus. Psy­cho­log­i­cal fac­tors are rel­e­vant since a placebo may alter pain per­cep­tion, for in­stance. But the con­tri­bu­tion of psy­cho­log­i­cal ef­fects is not set­tled and, gen­er­ally, there is a con­sen­sus that place­bos them­selves do not im­prove dis­ease in any ob­jec­tive way.

Rather, other fac­tors ex­plain the ob­served im­prove­ment, such as RTM. There are two dis­tinct cases: one in which the dis­ease is ex­pected to nat­u­rally re­solve for most peo­ple, such as a com­mon cold; an­other in which the dis­ease may be­come or al­ready is chronic and usu­ally does not re­solve with­out in­ter­ven­tion. In the first case, the placebo ef­fect is sim­ply the nat­ural course of the dis­ease.

When deal­ing with chronic ill­ness, symp­toms os­cil­late. Let’s say we’re mea­sur­ing pain. The cor­re­la­tion be­tween pain in con­sec­u­tive weeks is not per­fect, so RTM is at play. Even with no im­prove­ment of the un­der­ly­ing con­di­tion, weeks of very high pain will likely be fol­lowed by weeks of more mod­er­ate (av­er­age) pain.

Pa­tients are more likely to seek med­ical help or even to en­roll in clin­i­cal tri­als when their symp­toms are at their worst. This is a form of se­lec­tion bias, which is an­other prob­lem en­tirely, but it can greatly en­hance the ob­served ef­fect of RTM by se­lect­ing pa­tients with un­usu­ally bad symp­toms. The op­po­site is also true. If we ac­tively seek pa­tients with rheuma­toid arthri­tis in pe­ri­ods of ex­cep­tion­ally low pain, they will likely ex­pe­ri­ence more pain in sub­se­quent weeks, re­gard­less of the treat­ment.

Fooled by re­gres­sion to the mean

There is noth­ing causal in RTM. Good test scores do not pro­duce lower scores, ter­ri­ble prof­its do not pro­duce bet­ter re­sults in the next quar­ter. How­ever, it’s tempt­ing and makes in­tu­itive sense to in­ter­pret these phe­nom­ena as causal re­la­tion­ships. In fact, it’s tempt­ing to see causal­ity every­where, but we should be cau­tious.

When­ever we make a mea­sure­ment, take an ac­tion to in­flu­ence it, and mea­sure it again RTM is at play. This is com­monly seen in pun­ish­ment and re­ward strate­gies. Using sports re­sults as an ex­am­ple, luck and other ran­dom fac­tors are al­ways at play, so there is im­per­fect cor­re­la­tion be­tween two sub­se­quent per­for­mances of the same ath­lete. As we’ve seen above, chances are that very bad re­sults will be fol­lowed by bet­ter ones and vice-​versa, re­gard­less of pun­ish­ment or re­ward.

Even though it might seem su­per­fi­cially sim­ple, mea­sur­ing the causal ef­fect of any in­ter­ven­tion is sur­pris­ingly chal­leng­ing. Find­ing a con­trolled en­vi­ron­ment with as lit­tle ex­ter­nal in­flu­ence as pos­si­ble is al­ready a big chal­lenge, but sta­tis­ti­cal phe­nom­ena such as RTM still im­pair our abil­ity to reach causal con­clu­sions. This is of ex­treme rel­e­vance to many fields of sci­ence. For in­stance, vir­tu­ally all good-​quality bi­o­log­i­cal re­search uses con­trol groups (such as placebo groups), but this is not al­ways pos­si­ble.

In order to es­ti­mate the causal ef­fect of any­thing, we need to com­pare the world in which the in­ter­ven­tion oc­curred with the world in which it didn’t. We call the lat­ter the coun­ter­fac­tual world Strictly speak­ing, the coun­ter­fac­tual world doesn’t exist. When ex­per­i­men­tal de­signs with con­trol groups are pos­si­ble, we rely on big num­bers or good sam­pling to as­sume that both groups are sim­i­lar enough to be com­pared. But in fields such as eco­nom­ics and so­ci­ol­ogy it’s rarely pos­si­ble to cre­ate such a con­trol group.

Even though there are sta­tis­ti­cal workarounds for the lack of a plau­si­ble coun­ter­fac­tual, they are out of reach in every­day life. We should be aware that causal­ity is hard to prove and many fac­tors, one of which is RTM, may ex­plain the ap­par­ent ef­fect of our in­ter­ven­tions.

Con­clu­sion

Re­gres­sion to the mean is every­where. It can eas­ily fool our­selves into see­ing causal­ity where there is none. But re­gres­sion to the mean it­self is not causal, that is, there is noth­ing caus­ing the re­turn to the av­er­age value — it is a byprod­uct of im­per­fect cor­re­la­tion.