Exploring Fractals With Pytorch

Fr­a­cLac is a great pack­age for frac­tal analy­sis in Im­ageJ. Un­for­tu­nately, no sim­i­lar Python pack­age is avail­able. There are pieces of code that per­form the box-​counting al­go­rithm.

Most im­ple­men­ta­tions use the numpy reduceat func­tion. How­ever, this does not scale well, es­pe­cially in 3 di­men­sions. Thus, here we use Py­Torch to make use of GPU per­for­mance on 3D frac­tal analy­sis.

Gen­er­at­ing Frac­tals

I used the quin­tic for­mula to gen­er­ate a three-​dimensional Man­del­bulb pseu­do­frac­tal. The params vari­able can be freely changed to gen­er­ate dif­fer­ent Man­del­bulbs. Numba just-​in-​time com­piler is used to make the code more ef­fi­cient. Still, it is quite in­ef­fi­cient.

import numpy as np
from copy import deepcopy as dc
from numba import jit

@jit
def mandelbrot(x, y, z, x0, y0, z0, maxiter, params):
    A, B, C, D = params
    for n in range(maxiter + 1):
        if abs(x - x0) + abs(y - y0) + abs(z - z0) > 2:
            return n
        x = x**5 - 10*(x**3)*(y**2 + A*y*z + z**2) + 5*x*(y**4 + B*(y**3)*z + C*(y**2)*(z**2) + B*y*(z**3) + z**4) + D*(x**2)*y*z*(y+z) + x0
        y = y**5 - 10*(y**3)*(x**2 + A*x*z + z**2) + 5*y*(z**4 + B*(z**3)*x + C*(z**2)*(x**2) + B*z*(x**3) + x**4) + D*(y**2)*z*x*(z+x) + y0
        z = z**3 - 10*(z**3)*(x**2 + A*x*y + y**2) + 5*z*(x**4 + B*(x**3)*y + C*(x**2)*(y**2) + B*x*(y**3) + y**4) + D*(z**2)*x*y*(x+y) + z0
    return 0

# Draw our image
@jit
def mandelbrot_set(xmin, xmax, ymin, ymax, zmin, zmax, w, h, d, maxiter, params):
    r1 = np.linspace(xmin, xmax, w)
    r2 = np.linspace(ymin, ymax, h)
    r3 = np.linspace(zmin, zmax, d)
    n3 = np.empty((w, h, d))
    for i in range(w):
        for j in range(h):
            for k in range(d):
                x, y, z = r1[i], r2[j], r3[k]
                x0, y0, z0 = dc(x), dc(y), dc(z)
                n3[i,j, k] = mandelbrot(x, y, z, x0, y0, z0, maxiter, params)
    return (r1, r2, r3, n3)


def mandelbrot_image(dims, params, width = 20, height = 20, depth = 20, maxiter=64):
    xmin, xmax, ymin, ymax, zmin, zmax = dims
    dpi = 50
    img_width = dpi * width
    img_height = dpi * height
    img_depth = dpi * depth
    _, _, _, frac = mandelbrot_set(xmin, xmax, ymin, ymax, zmin, zmax, img_width, img_height, img_depth, maxiter, params)
    return frac

if __name__ == '__main__':
    dims = (-2, 2, -2, 2, -2, 2)
    params = (1, 0, 1, 0)
    frac = mandelbrot_image(dims, params, 10, 10, 10, 30)

Here we present an ex­am­ple with (1, 0, 1, 0) pa­ra­me­ters. The code to gen­er­ate an an­i­mated GIF with pyplot.imshow is pre­sented below:

import matplotlib.pyplot as plt
import matplotlib.animation as animation
from copy import deepcopy as dc

frac_img = dc(frac)
frac_img[frac_img < 2] = 0

fig = plt.figure()

# ims is a list of lists, each row is a list of artists to draw in the
# current frame; here we are just animating one artist, the image, in
# each frame
ims = []
for i in range(int(frac_img.shape[-1]/5)):
    im = plt.imshow(frac_img[:, :, i*5]**(1/2), animated=True, cmap = 'bone')
    ims.append([im])

ani = animation.ArtistAnimation(fig, ims, interval=75, blit=True,
                                repeat_delay=0)

ani.save('./frac_animation.gif', writer='imagemagick', fps = 30)

The square root is used to re­duce the image con­trast and en­hance vi­su­al­iza­tion. The image rep­re­sents a slid­ing slice of the image on the z-​axis, just like a to­mog­ra­phy.

Frac­tal Analy­sis

The box-​counting al­go­rithm is the most pop­u­lar method of frac­tal analy­sis. It con­sists of defin­ing scan­ning boxes (of a square shape) with ex­po­nen­tially in­creas­ing sizes and scan­ning through a bi­nary image. If an edge is de­tected in­side the cur­rent box, a count is added to the total.

This can be eas­ily gen­er­al­ized to three di­men­sions sub­sti­tut­ing squares for cubes.

By Prokofiev — Own work, CC BY-SA 3.0

This count is per­formed for each box size and the box slides through the image with a pre­de­fined stride, in our case, the stride was de­fined as half the box side. Using py­torch AvgPool3d func­tion, we can de­tect edges as fol­lows: if the av­er­age pool­ing is 0, there is no edge; if it’s 1, the ob­ject com­pletely fills the box, with­out edges. Thus, a pool­ing be­tween 0 and 1 means that there’s an edge. This can be achieved with the fol­low­ing code:

stride = (int(size/2), int(size/2), int(size/2))
pool = AvgPool3d(kernel_size = (size, size, size), stride = stride, padding = int(size/2))
# Performs optimized 3D average pooling for box-counting
S = pool(image)

Where size is the di­men­sion of the image.

Frac­tal Di­men­sion

The frac­tal di­men­sion is an es­ti­mate of the com­plex­ity of a frac­tal as a func­tion of scale. That is, it mea­sures how com­plex the pat­tern is by using pro­gres­sively smaller scales. You should check the Wikipedia page for frac­tal di­men­sion if you want to know more.

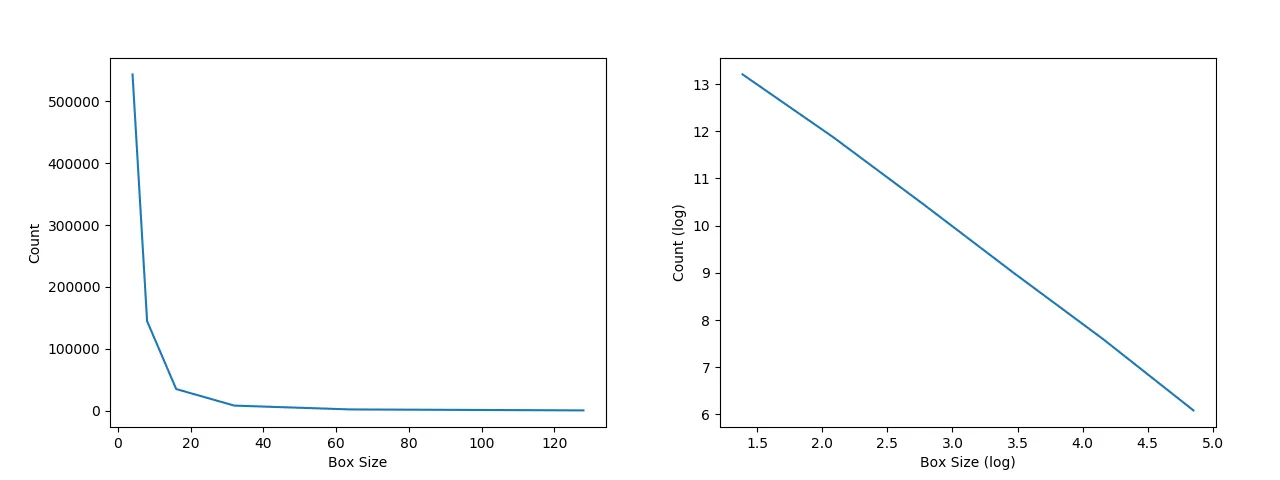
An es­ti­ma­tor of the frac­tal di­men­sion of an image can be ob­tained through the box-​counting al­go­rithm: the counts should fol­low a power law dis­tri­b­u­tion in per­fect frac­tal im­ages, that is, the num­ber of counts in­crease ex­po­nen­tially as the box size goes down. The frac­tal di­men­sion es­ti­ma­tor from box-​counting (Db) is the op­po­site of the slope of a lin­ear reg­gres­sion that takes as in­puts the nat­ural log of counts and the nat­ural log of box sizes. Ap­ply­ing the log trans­for­ma­tion to both axis trans­forms a power law re­la­tion­ship into a lin­ear one. The next two im­ages show the ef­fect of the log trans­for­ma­tion:

La­cu­nar­ity

La­cu­nar­ity is an­other use­ful mea­sure to ex­plore fractal-​like pat­terns. It is a mea­sure of “gap­pines” and, more gen­er­ally, of het­ero­gene­ity (ro­ta­tional in­vari­ance). In­tu­itively, it can be thought as a mea­sure of how dense a pat­tern is and how self-​similar it is when sub­jected to spa­tial trans­for­ma­tions. It can be es­ti­mated with the box-​counting al­go­rithm using the fol­low­ing for­mula:

where $\varepsilon$ is the box size and $g$ is the ori­en­ta­tion. More­over, $\sigma$ and $\mu$ are the standard-​error and mean num­ber of pix­els per box, recpec­tively.

Full code

The com­plete code for frac­tal analy­sis (im­ple­ment­ing the Frac­tal class) is pre­sented below:

from scipy.stats import linregress
from torch.nn import AvgPool3d
import torch

class Fractal:

    def __init__(self, Z, threshold = 1):

        # Set the default tensor as CUDA Tensor
        # If you don't have a CUDA GPU, remove all 'cuda' from the lines below
        torch.set_default_tensor_type('torch.cuda.FloatTensor')

        # Make the array binary
        self.Z = np.array((Z > threshold), dtype = int)

        # Get the list of sizes for box-counting
        self.sizes = self.get_sizes()

        # Perform box-counting
        self.count, self.lac = self.get_count()

        # Get fractal dimensionality
        slope, _, R, _, self.st_er = linregress(np.log(self.sizes), np.log(self.count))
        self.Db = -slope
        self.Rsquared = R**2

        # Lacunarity measures
        self.mean_lac = np.mean(self.lac)
        # 1 is added to avoid log of 0
        self.lac_reg_coeff, _, R_lac, _, self.st_er_lac = linregress(np.log(self.sizes), np.log(self.lac + 1))
        self.Rsquared_lac = R_lac**2

        return None

    def get_sizes(self):

        # Minimal dimension of image
        p = min(self.Z.shape)

        # Greatest power of 2 less than or equal to p/2
        n = 2**np.floor(np.log(p/2)/np.log(2))

        # Extract the exponent
        n = int(np.log(n)/np.log(2))

        # Build successive box sizes (from 2**n down to 2**1)
        sizes = 2**np.arange(n, 1, -1)

        return sizes

    def get_count(self):

        # Pre-allocation
        counts = np.empty((len(self.sizes)))
        lacs = np.empty((len(self.sizes)))
        index = 0

        # Transfer the array to a 4D CUDA Torch Tensor
        temp = torch.Tensor(self.Z).unsqueeze(0)

        # Box-counting
        for size in self.sizes:
            # i is a variable to perform box-counting at multiple orientations
            i = 0
            count_u = 0
            lac = 0

            while i in range(4) and ((i*(size/4) + size) < min(self.Z.shape)-1):
                temp = temp[:, i:, i:, i:]
                stride = (int(size/2), int(size/2), int(size/2))
                pool = AvgPool3d(kernel_size = (size, size, size), stride = stride, padding = int(size/2))
                # Performs optimized 3D average pooling for box-counting
                S = pool(temp)
                count = torch.sum(torch.where((S > 0) & (S < 1), torch.tensor([1]), torch.tensor([0]))).item()

                # Add to box counting
                count_u += count

                # Calculate Lacunarity
                u = torch.mean(S).item()
                sd = torch.std(S, unbiased = False).item()

                # 0.1 is added to avoid possible error due to division by 0
                lac += (sd/(u+0.1))**2
                #print(lac)
                i += 1

            # Avoid division by 0
            if i != 0:
                count_u *= 1/i
                lac *= 1/i

            # Results are given as an average for all orientations
            counts[index] = count_u
            lacs[index] = lac
            index += 1

        return counts, lacs

First, the array is con­verted to a bi­nary one ac­cord­ing to a pro­vided thresh­old. Fol­low­ing, the get_sizes func­tion cal­cu­lates box sizes as pow­ers of 2, with­out ex­ceed­ing half the size of the array’s smaller di­men­sion.

The get_count func­tion per­forms the magic. The while loop en­sures that a max­i­mum of 4 ori­en­ta­tions is used for each box size to de­crease bias. Then, the AvgPool3d com­bined with the torch.where func­tions per­form the box-​counting, which is added to the count_u vari­able for each it­er­a­tion. Also, for each it­er­a­tion, a la­cu­nar­ity value is cal­cu­lated. The final count value is just the sum of all ori­en­ta­tions for each size, while the final la­cu­nar­ity value is the av­er­age for all ori­en­ta­tions at a given box size.

The frac­tal shown in the GIF image has a 2.05795 frac­tal di­men­sion and a 1.19497 mean la­cu­nar­ity. If you want a more in-​depth view of frac­tal analy­sis, con­sider read­ing this ar­ti­cle.