Recently, I stumbled upon a very interesting blog post and a Reddit thread about an algorithm to play battleship in the best possible way. The blog post, however, does not explain how probabilities are calculated. So, I decided to give it a try and write my own code for this problem.
Disclaimer: this is my first ever Python script. Thus, it’s not a masterpiece, and I’m sure there’s room for improvement.
Basic Code
I started by writing a code that sets the boards and prepares the game of human versus the computer. I won’t cover this section in much detail, as the code can be seen below. In a nutshell, the code places 5 ships of sizes 5, 4, 3, 3 and 2 squares on the board, making sure that they do not overlap (but they can touch each other). There’s also an input option for the difficulty, in which the easy mode corresponds to random guessing by the computer, while the hard mode uses the algorithm that we’ll develop.
board = []
for x in range(size):
board.append(["O"] * size)
ships = [5, 4, 3, 3, 2]
def create_ships(board, ships):
for ship in range(0, len(ships)):
valid = False
while not valid:
row = randint(1, 10 - ships[ship])-1
col = randint(1, 10 - ships[ship])-1
orient = randint(0, 1)
if orient == 0:
orientation = "v"
else:
orientation = "h"
valid = validate(board, ships[ship], row, col, orientation)
board = place_ship(board, ships[ship], orientation, row, col)
return board
def place_ship(board, ship, orientation, x, y):
if orientation == "v":
for i in range(0, ship):
board[x+i][y] = 1
elif orientation == "h":
for i in range(ship):
board[x][y+i] = 1
return board
def validate(board, ship, row, col, orientation):
if orientation == "v" and row + ship > 10:
return False
elif orientation == "h" and col + ship > 10:
return False
else:
if orientation == "v":
for i in range(0, ship):
if board[row + i][col] != 0:
return False
elif orientation == "h":
for i in range(0, ship):
if board[row][col + i] != 0:
return False
return TrueA Simple Algorithm
So far so good! Now the computer will make its first guess. Following the idea of the blog post, the algorithm enters a hunt mode until it hits a ship. The idea is to recursively place the ships (both horizontally and vertically) on the opponent’s board and see if there is a miss (indicated by an X) in the range of squares covered by that ship in that hypothetical position. If there is no X, then the algorithm sums 1 to all these squares. In the end, we get a matrix of numbers that are standardized to a maximum of 1 (and minimum of 0) in which the highest values indicate a higher probability to encounter a ship in that spot.
import numpy as np
def probability_hunt(board, ships, size, hit):
prob = np.zeros((size, size))
for ship in ships:
verify = []
verify.append(['O'] * ship)
for row in range(0, len(board[0])):
for k in range(0, len(board[0]) - ship + 1):
if 'X' not in board[row][k:k + ship]:
prob[row, k:k + ship] += 1
for col in range(0, len(board[0])):
column = []
for row in range(0, len(board[0])):
column.append(board[row][col])
for j in range(0, len(board[0]) - ship + 1):
if 'X' not in column[j:j + ship]:
prob[j:j + ship, col] += 1
prob = np.divide(prob, np.amax(prob))
for i in hit:
prob[i[0], i[1]] = 0.1
for row in range(0, len(board[0])):
for i in range(0, len(board[0])):
if board[row][i] == 'B':
prob[row, i] = 0
return probThe solution of working with a board as a list of lists is far from elegant, and numpy arrays might have been a better option. However, to be honest, I had already written this piece of code by the time I thought about this, and it works!
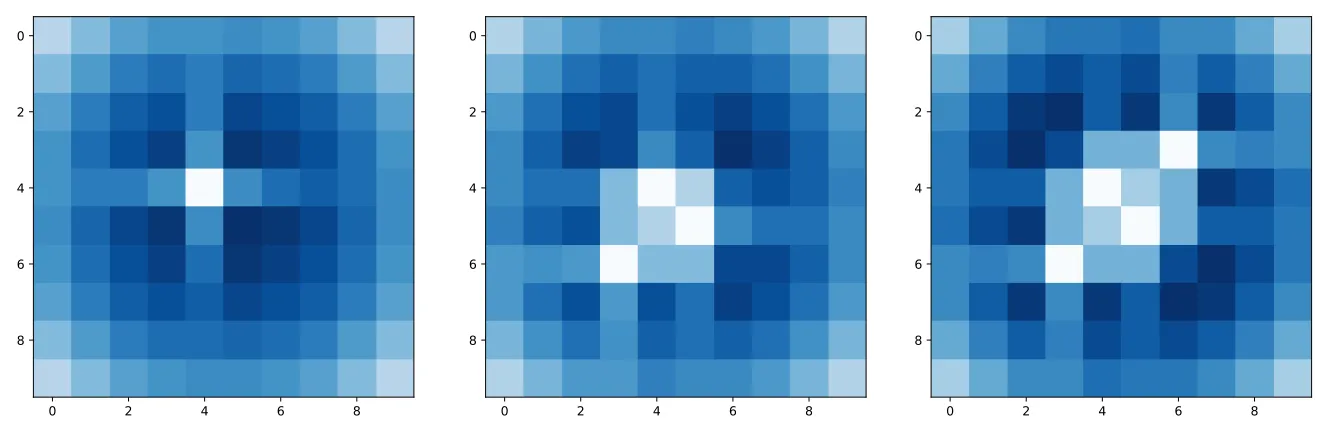
Considering a standard board of 10x10 squares, let’s see a few examples to understand how the algorithm is working so far. In the beginning of the game, the computer will always guess a square close to the center of the board, as there’s a higher probability that a ship is there (compared to the edges). It’s very important to consider that the ships are placed randomly, and a human placing ships might even prefer the edges of the board. The function returns the following matrix:
After each incorrect guess, we recalculate the matrix considering the new information. Below are some examples:
When the computer finally hits a ship, the algorithm enters an attack mode. This time, however, I decided to spice things up a little: in the blog post, the opponent should inform the length of the hit ship and when it sunk. In this version of the game, however, neither is required. I thought this would just save some coding, but it turned out to make the game much harder.
In the first version of the algorithm, when the computer hits a ship, it enters into attack mode. This function calculates all the possible ship configurations in which the hit(s) square(s) is(are) covered by a ship. In the original blog post, the computer would know when to switch back to hunt mode — it simply did it when the ship being attacked sunk. However, in the absence of this information, I adopted the (completely arbitrary yet reasonable) heuristic of returning to hunt mode after 3 consecutive misses. The code for this is:
def probability_attack(board, hit, ships, size):
prob = np.zeros((size, size))
for ship in ships:
for row in range(0, len(board[0])):
for i in hit:
if i[0] == row:
for k in range(i[1] - ship + 1, i[1] + 1):
if k >= 0:
if 'X' not in board[row][k:k + ship]:
if (k + ship) < len(board[0]):
prob[row, k:k + ship] += 1
for col in range(0, len(board[0])):
column = []
for i in hit:
if i[1] == col:
for k in range(i[0] - ship + 1, i[0] + 1):
if k >= 0:
for row in range(0, len(board[0])):
column.append(board[row][col])
if 'X' not in column[k:k + ship]:
if (k + ship) < len(board[0]):
prob[k:k + ship, col] += 1
for i in hit:
prob[i[0], i[1]] = 0
for row in range(0, len(board[0])):
for i in range(0, len(board[0])):
if board[row][i] == 'B':
prob[row, i] = 0
return probThis code produces some beautiful matrices, as shown in examples below. Again, the computer chooses the highest value in the matrix and if there’s a tie the choice is randomly sampled from the tied highest values. In order to understand how this works, let’s go through an example:
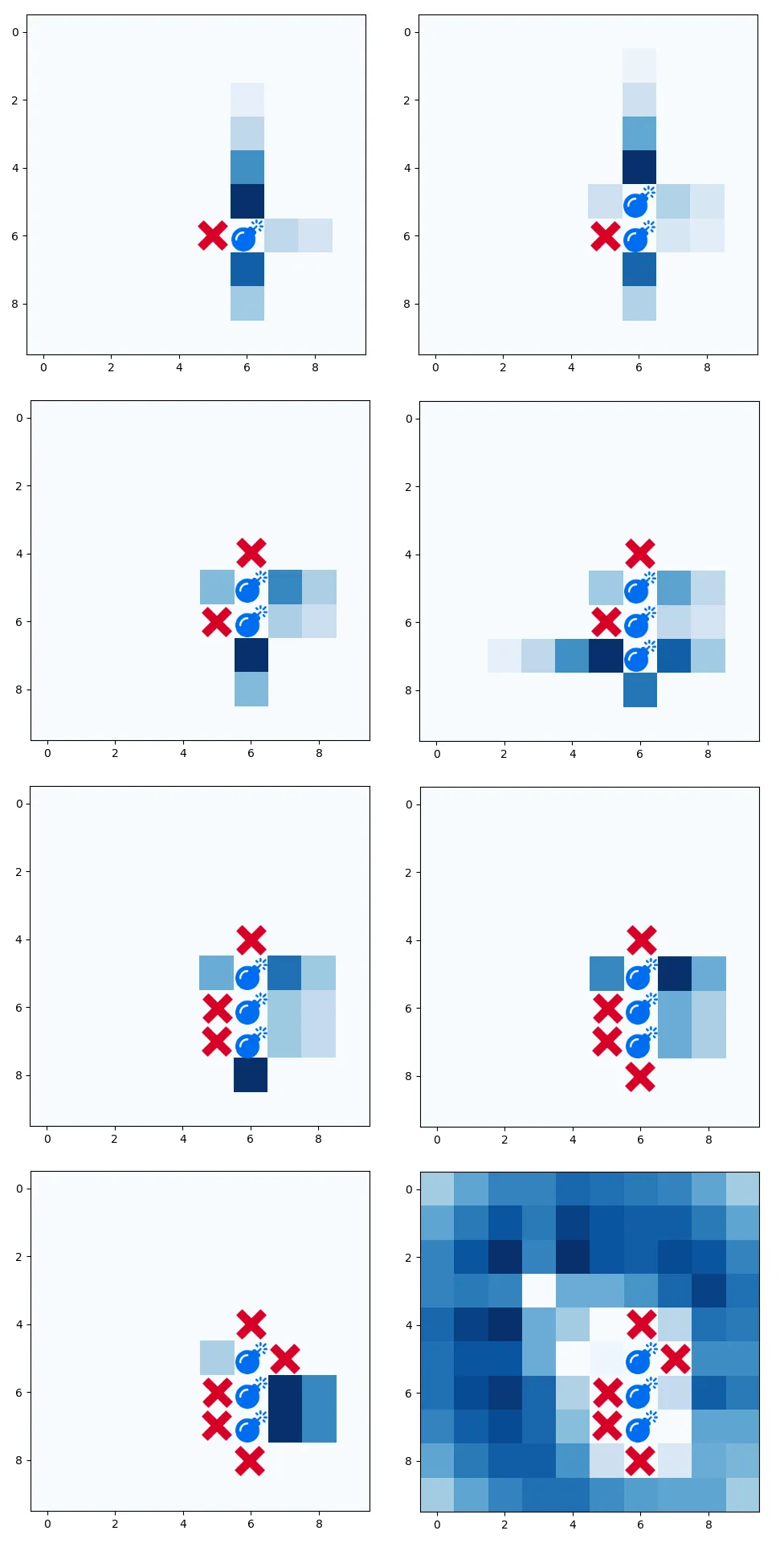
Icons made by Freepik from Flaticon are licensed by Creative Commons BY 3.0
While still in hunt mode, the computer hit one ship. In the first matrix, we can see the estimated probabilities to whether the adjacent squares also contain a ship. The computer picks the highest value and hit the ship again! But in its next move, the computer misses. This changes the look of the matrices, and the computer begins to explore downwards. Again, it’s a hit! However, as we don’t know the size of the ship being hit, the computer iteratively consider all ships to estimate these values; thus, although the intuitive approach would be to keep exploring downwards, the computer decides to go left, as bigger ships could fit better in that direction compared to the small space of 2 squares downwards. It is, nonetheless, a miss. This process keeps going until 3 consecutive misses. Then, the computer goes back to hunt mode, as seen in the last matrix.
Fine-Tuning
The first issue with this approach is already visible: the algorithm avoids the edges of the table, making counterintuitive shifts in the orientation of its predictions. To tackle this issue, I’ve created a list variable hit, in which the computer appends its correct guesses recursively. The list is emptied when returning to hunt mode. The code checks the orientation of the collinear streak of hits and the values in this row or column are multiplied by 2. The multiplier is arbitrary and was chosen by trial and error, but I’m sure better approaches could estimate a more relevant value.
hit.append([guess_row, guess_col])
if len(hit) > 1 and hit[-2][0] == hit[-1][0]:
prob[hit[-1][0], :] = np.prod([prob[hit[-1][0], :], 3])
elif len(hit) > 1 and hit[-2][1] == hit[-1][1]:
prob[:, hit[-1][1]] = np.prod([prob[:, hit[-1][1]], 3])Another issue is that the computer makes unnecessary misses when a situation similar to the sixth matrix above happens: when a streak of collinear hits has misses in both its ends, it’s very likely that the ship has sunk. Still, ships cannot go over one another, but they can (and do) touch each other. Therefore, creating a constraint that does not let the algorithm change the orientation of its guesses could (and in fact does) have a negative impact over its performance.
The proposed solution is to create yet another probability estimating function. Using again the hit variable, the code checks again the orientation of the collinear streak of hits and if the sum of probabilities for the corresponding row or column is 0. This can only happen in a situation very similar to the one posed in the sixth matrix of the figure above: there’s a streak of 3 vertical hits, but they are followed by misses in both of its ends. Therefore, the sum of all the values of that column is 0, strongly suggesting that the ship has sunk or that there’s another ship touching the already found one. If this condition is true, a variable named count is set to 1 and the probability matrix is calculated as the average of the matrices returned by the probability_hunt and the probability_attack functions. In this way, the algorithm returns sooner to hunt mode — avoiding unnecessary misses — while keeping in part the values calculated by the attack function.
def probability_mixed(board, hit, count, ships, size):
prob = probability_attack(board, hit, ships, size)
prob2 = probability_hunt(board, ships, size, hit)
count = 0
if (
len(hit) > 1 and hit[-2][0] == hit[-1][0]
and sum(prob[hit[-1][0], :]) == 0
):
count = 1
elif (
len(hit) > 1 and hit[-2][1] == hit[-1][1]
and sum(prob[:, hit[-1][ 1]]) == 0
):
count = 1
if len(hit) > 1 and hit[-2][0] == hit[-1][0]:
prob[hit[-1][0], :] = np.prod([prob[hit[-1][0], :], 3])
elif len(hit) > 1 and hit[-2][1] == hit[-1][1]:
prob[:, hit[-1][1]] = np.prod([prob[:, hit[-1][1]], 3])
if np.amax(prob) > 0:
prob = np.divide(prob, np.amax(prob))
prob = prob * (1 - (1/2) * count)
prob2 = prob2 * (1/2) * count
prob3 = np.add(prob, prob2)
return prob3This seems like a reasonable heuristic that allows finding touching ships while avoiding extra misses. However, it also exacerbates another problem: while the probability_mixed function is below the 3 misses threshold, it can hit another ship, unrelated to the previous hits, specially when we use the mixed matrix. This creates a weird situation: the computer may not leave the attack mode for a very long time, making the hit variable absurdly long. So, you may have guessed it, we are going to create yet another heuristic. It seems reasonable that the most recent hits should have a bigger weight when estimating the matrix. However, this cannot be overdone, or a shift in direction of guesses would become highly unlikely — jeopardizing the algorithm’s performance. So, an additional term which came to my mind is the Euclidean distance of one hit to the next one. As the distance increases, there’s a much higher probability that we’re not hitting one single ship, but rather two or more. Thus, joining these two ideas — with yet another arbitrary value of 1.5 relative importance to the distance compared to the index (newer versus older hits), a new empirical version of the probability_attack function arises:
def probability_attack(board, hit, ships, size):
prob = np.zeros((size, size))
for ship in ships:
for row in range(0, len(board[0])):
for i in hit:
if i[0] == row:
for k in range(i[1] - ship + 1, i[1] + 1):
if k >= 0:
if 'X' not in board[row][k:k + ship]:
if (k + ship) < len(board[0]):
prob[row, k:k + ship] += (1\
- 0.1 * (1.5 * distance(hit, i) - hit.index(i)))
for col in range(0, len(board[0])):
column = []
for i in hit:
if i[1] == col:
for k in range(i[0] - ship + 1, i[0] + 1):
if k >= 0:
for row in range(0, len(board[0])):
column.append(board[row][col])
if 'X' not in column[k:k + ship]:
if (k + ship) < len(board[0]):
prob[k:k + ship, col] += (1\
- 0.1 * (1.5 * distance(hit, i) - hit.index(i)))
for i in hit:
prob[i[0], i[1]] = 0
for row in range(0, len(board[0])):
for i in range(0, len(board[0])):
if board[row][i] == 'B':
prob[row, i] = 0
return prob
def distance(hit, i):
if hit.index(i) == (len(hit) - 1):
dist = 0.1
return dist
else:
horizontal = i[0] - hit[hit.index(i) + 1][0]
vertical = i[1] - hit[hit.index(i) + 1][1]
dist = sqrt(horizontal ** 2 + vertical ** 2)
return distI think there are still two unsolved problems with this code: it does not take into account that ships cannot overlap. I tried to make two functions to detect adjacent ships and take into account this rule, which became the ridiculously long if statements below:
from copy import deepcopy as dc
pboard = dc(board)
def adj_rows(k, row, board, pboard, ship):
if k > 0:
if (row > 0 and row < 9 and board[row][k - 1] == 'B'
and board[row - 1][k - 1] == 'B' and board[row + 1][k - 1] == 'B')
or (row == 0 and board[row][k - 1] == 'B' and board[row + 1][k - 1] == 'B')
or (row == 9 and board[row - 1][k - 1] == 'B' and board[row][k - 1] == 'B'):
pboard[row][k - 1] == 'X'
pboard[row - 1][k - 1] == 'X'
pboard[row + 1][k - 1] == 'X'
if (k + ship) < len(board[0]):
if (row > 0 and row < 9 and board[row][k + ship] == 'B'
and board[row - 1][k + ship] == 'B' and board[row + 1][k + ship] == 'B')
or (row == 0 and board[row][k + ship] == 'B' and board[row + 1][k + ship] == 'B')
or (row == 9 and board[row - 1][k + ship] == 'B' and board[row][k + ship] == 'B'):
pboard[row][k + ship] == 'X'
pboard[row - 1][k + ship] == 'X'
pboard[row + 1][k + ship] == 'X'
return pboard
def adj_cols(k, col, board, pboard, ship):
if k > 0:
if (col > 0 and col < 9 and board[k - 1][col - 1] == 'B'
and board[k - 1][col] == 'B' and board[k - 1][col + 1] == 'B')
or (col == 0 and board[k - 1][col] == 'B' and board[k - 1][col + 1] == 'B')
or (col == 9 and board[k - 1][col - 1] == 'B' and board[k - 1][col] == 'B'):
pboard[k - 1][col - 1] = 'X'
pboard[k - 1][col] = 'X'
pboard[k - 1][col] = 'X'
if (k + ship) < len(board[0]):
if (col > 0 and col < 9 and board[k + ship][col - 1] == 'B'
and board[k + ship][col] == 'B' and board[k + ship][col + 1] == 'B')
or (col == 0 and board[k + ship][col] == 'B' and board[k + ship][col + 1] == 'B')
or (col == 9 and board[k + ship][col - 1] == 'B' and board[k + ship][col] == 'B'):
pboard[k + ship][col - 1] = 'X'
pboard[k + ship][col] = 'X'
pboard[k + ship][col] = 'X'
return pboardThis hideous code, however, worsened the algorithm’s performance, so the problem remain unsolved.
The other one is that the algorithm does not take into account the probability that a certain ship has already sunk and includes all ships equally in all its calculations. Some attempts to create an estimator to weight each ship contribution did not succeed as well.
Evaluating Performance
The number of turns required to complete a game (sink all ships) was recorded for 5000 simulations. I’ve estimated the empirical cumulative distribution with a Gaussian kernel for each version of the code. Version 1 corresponds to random guessing. Version 2 only guesses through the hunt mode; version 3 includes the first version of the attack mode; version 4 includes the heuristics of the mixed matrix; and version 5 is the final one with the distance heuristics.
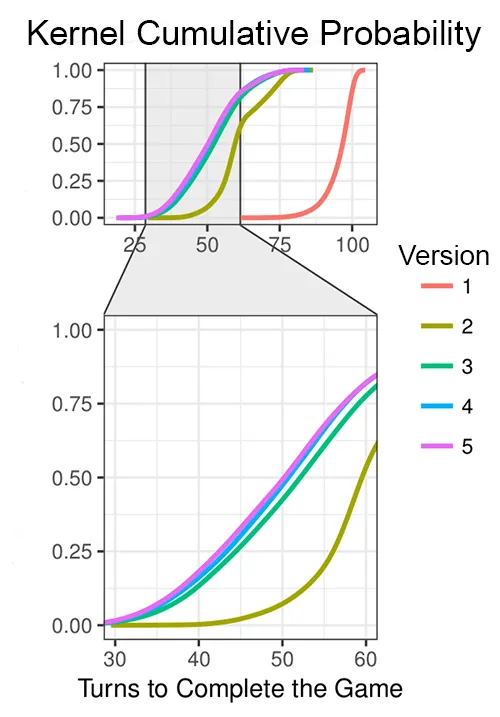
The improvement was substantial until the third version, which included the basic hunt/attack alternating algorithm. However, further improvement was very subtle. The Hedge’s g effect size estimator was used to compare each version with the next one, yielding the following values: versions 1 vs 2: ; versions 2 vs 3: ; versions 3 vs 4: ; versions 4 vs 5: . Thus, it seems that until versions 4 there was significant improvement; however, the change between versions 4 and 5 is very subtle, suggesting that maybe the distance heuristic is not as good as it may look.
The Python script for an interactive version of Battleship implementing this algorithm is available through this GitHub Repository.
This algorithm is not perfect, and I’m sure there’s room for improvement. If you have any ideas, please leave a comment!